Hacer click en la figura para ver el detalle.
Ver mas:
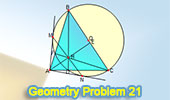
Problema de Geometria 21
Coleccion de Problemas
Problemas en Ingles
Nivel: Educacion Secundaria, Academia, Preparatoria, Bachillerato, College
Triangulos, Poligonos, Circulos, Puntos Notables, Congruencia, Semejanza, Relaciones Metricas, Areas, Transformaciones

1) AH*AE=AM^2
ResponderEliminar(El cuadrilatero EDCH es ciclico E=D=90º , la potencia de A respecto de dicha circunferencia es AH*AE=AD*AC , pero este ultimo valor es la potencia de A respecto de de la circunferncia dato del problema , que es a su vez =AM^2)
2)El cuadrilatero AMON es ciclico y E pertenece a esa circunferencia ( AM es perpendicular a OM ; radio y tangente , por la misma razón AN y ON , => MAON son conciclicos) en esta circunferncia AO es el diametro pues se ve bajo 90º desde M y N, pero el ángulo AEO =90º , pues AE es la altura => desde E se ve el diametro AO BAJO 90º => E está en la circunferencia
Consideremos la inversión de centro A y potencia AM^2=AN^2 , la circunferencia de diametro AB es doble ...
La inversa de la recta MN será una circunferencia que pasará pòr A y por M y N (ya que estos son puntos dobles) pero en esta circunferencia está E (segun 2); pero segun 1) en esta inversion E es el inverso de H , asi H está en la recta inversa de la circunferencia AMNOE, es decir lsa recta MN => M,N,H están alineados
buena solución
ResponderEliminarpara que M,H,N estén alineados, sólo bastará demostrar que mpor teorema recipróco al de antiparalelas se concluye que mmmAO y MN forman un ángulo recto, por lo cual mm<AMN=m<ANM=c. por lo tanto el cuadrilátero AMEN es inscriptible, por lo cual queda demostrado que los puntos M, H y N son coliniales.
ResponderEliminarHaré la solución paso a paso.
ResponderEliminar1)Teorema:Si por un punto A exterior a una circunferencia se trazan las tangentes AM y AN (M y N en la circunferencia), además la perpendicular AE al diámetro BC, el cuadrilátero AMEN será inscriptible(Estoy usando el gráfico dado)
cuando escribo la solución no aparece todo el texto, asi que si desean la solución pueden mandarme un correo a gallo1685@hotmail.com
ResponderEliminarsaludos
Partiremos de dos propiedades previas.
ResponderEliminar1) A partir de un punto A, exterior a una circunferencia de centro O se trazan las tangentes AM y AN ( M y N sobre esta) y la perpendicular AE al diámetro BC (E en BC), se cumple que el cuadrilátero AMEN es inscriptible y AE es bisectriz del ángulo MEN.
* Demostración:
Se trazan OM, ON y AO.
El cuadrilátero AOEN es inscriptible ( m < AEO = m < ONA = 90°) ,entonces m < AON = m < AEN = Ɵ.......1
El cuadrilátero AMON es inscriptible ( m < AMO = m < ONA = 90°)y es un trapezoide simétrico(se entiende que AE es eje de simetría), entonces m < AMN = m < AON = Ɵ.......2
De (1) y (2), el cuadrilátero AMEN es inscriptible y por
2) Sea un triángulo ABC y BD una ceviana interior tal que AB^2 = (AD)(AC), se concluye que m < ABD = m < ACB.
Demostración:
Se nota que el ángulo BAC es común para los triángulos ABD y ACB. Del dato,ordenando convenientemente, se tiene AB/AD=AC/AB, con lo cual podemos afirmar que los triángulos ABD y ACB son semejantes, siendo m < ABD = m < ACB por tratarse de elemnetos homólogos.
Ahora resolveremos el problema.
Por la propiedad (1), AE es la bisectriz del ángulo MEN => m < AEM = m < AEN = ϕ.
Por el teorema de la tangente , tenemos:
AN^2 = (AD)(AC).....a
El cuadrilátero DHEC es inscriptible, entonces por el teorema de la secante , se tiene:
(AD)(AC) = (AH)(AE)
reemplazando en (a) se tiene:
AN^2 = (AH)(AE).....(m)
Por la propiedad (2):
En (m): en el triángulo ANE, m < ANH = m < AEN = ϕ.
Dado que el cuadrilátero AMEN es inscriptible , AE y MN son sus diagonales, por rebote la m < AMN = m < AEN = ϕ, pero m < AMH = ϕ, por lo tanto los puntos M,H y N deben ser colineales
Solucion enviada por Alejandro Astudillo A. de Santiago, Chile en
ResponderEliminarProblema 21, Solucion 1