Hacer click en la figura para ver el enunciado y el grafico completo del problema 44.
Ver mas:
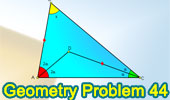
Problema de Geometria 44
Nivel: Educacion Secundaria, Academia, Preparatoria, Bachillerato, College
Triangulos, Poligonos, Circulos, Puntos Notables, Congruencia, Semejanza, Relaciones Metricas, Areas, Transformaciones

Hola,soy yo otra ves,para resolver el problemita,lo primero que tenemos que hacer es ubicar un punto "D" (exterior relativo al lado BC),tal que ABDC sea un romboide,entonces podemos decir que m< CBD = 2α , m< BDC = 4α , m< BCD = x ;y tambien de que AC = BD , AB = DC
ResponderEliminarLuego,en el triangulo BDC,trazamos la ceviana
interior DE , tal que m< BDE = α , entonces
m< EDC = 3α , luego podemos notar rapidamente
que la m< DEC = 3α , entonces el triangulo EDC,
es isoceles,verdad,entonces DC = EC
Luego si nos damos cuenta,los triangulos BED
y ADC,son congruentes por el caso A.L.A , verdad
entonces,en el triangulo ADC,como al angulo "2α"
se le opone un segmentito,en el triangulo BED,
al angulo "2α",tambien se le debe oponer,un
segmentito,que mida lo mismo que DC,verdad.
Entonces,con esto estarimos demostrando,que el
triangulo EDC,es esqulatero,verdad, y si
nos damos cuenta,uno de sus angulos es "x"
--> x = 60º
Bueno eso es todo !!
Saludos desde Lima - Peru
Bien jugado. ¿Cómo se te ocurrió?
ResponderEliminar