domingo, 26 de abril de 2009

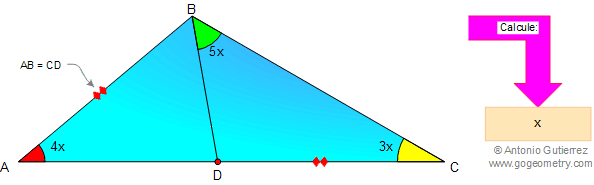
Problema 13: Triangulo, Ángulos, Ceviana, Congruencia

Problema propuesto
La figura muestra el triangulo ABC, ángulo A = 4x, ángulo C = 3x, ángulo CBD = 5x, y AB = CD, Calcule x.

Problema 13: Triangulo, Ángulos, Ceviana, Congruencia.

Ver mas:
Problema de Geometria 13, Coleccion de Problemas

Nivel: Educacion Secundaria, Academia, Preparatoria, Bachillerato, College
Posted by Antonio Gutierrez at 10:48
Labels: , , ,

5 comentarios:

  1. javier29 de octubre de 2009, 0:39

    la respuesta es 10

    ResponderEliminar
  2. Anónimo28 de marzo de 2010, 21:55

    Hola,soy yo otra ves,veamos :

    1) Para comenzar,podemos notar rapidamente
    que el angulo BDA = 8x,ahora en el triangulo ABD,trazamos la ceviana interior BE,tal que el angulo BED = 8x --> el angulo ABE = 4x

    2) Ahora en el triangulo BDC,ubicamos un punto "F" exterior relativo al lado BC,tal que el angulo FDC = 4x y el angulo FCB = x

    3) Ahora si nos damos cuenta los triangulos ABE y DFC son congruentes verdad,entonces :
    AE = EB = a (en el triangulo ABE),pero como
    EB = BD --> BD = a,pero como dichos triangulos
    son congruentes,entonces DF = FC = a ,ahora prolongamos FD hasta un punto "G",entonces el angulo EDG = 4x,pero como el triangulo BDF es isoceles y el angulo BDG = 12x,entonces el angulo BFD = 6x y el angulo FBC = x

    4) Ahora si nos damos cuenta el triangulo BFC es isoceles verdad,porque el angulo FBC = al angulo FCB,entonces FC = a,pero como FC = BF,entonces BF = a ,con esto estamos demostrando
    que el triangulo BDF es equilatero,entonces :
    6x = 60 ---> x = 10

    ResponderEliminar
  3. Antonio Gutierrez19 de octubre de 2011, 10:44

    Solucion enviada por Alejandro Astudillo A. de Santiago, Chile en
    Problema 13, Solucion 1

    ResponderEliminar
  4. Antonio Gutierrez31 de marzo de 2012, 16:45

    Solucion en video del problema 13 enviada por Eder Contreras y Cristian Baeza realizado en el Instituto de Matemáticas (IMA) de la Pontificia Universidad Católica de Valparaiso (PUCV), Chile.

    ResponderEliminar
  5. Anónimo11 de septiembre de 2019, 19:11

    Esta es mi solucion al problema:
    https://mega.nz/#!cpxh0KzQ!chYX0Bf-JVrGS71svEjf33p_0UVOwbrEEmnOH3toqVs

    Pedro Miranda

    ResponderEliminar

Suscribirse a: Enviar comentarios (Atom)