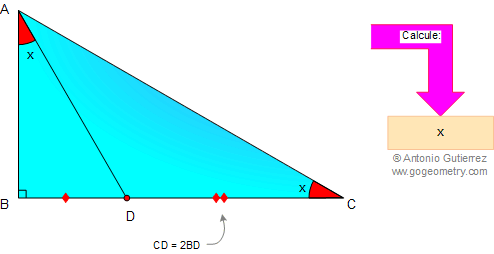
La figura muestra el triangulo rectángulo ABC, Si ángulo BAD = ángulo ACB = x y CD = 2BD, calcule x.
Ver mas:
Problema de Geometria 11, Coleccion de Problemas
Nivel: Educacion Secundaria, Academia, Preparatoria, Bachillerato, College
domingo, 26 de abril de 2009
Problema 11: Triangulo rectángulo, Ángulos, Ceviana, Trazos auxiliares
Problema propuesto
La figura muestra el triangulo rectángulo ABC, Si ángulo BAD = ángulo ACB = x y CD = 2BD, calcule x.
Ver mas:
Problema de Geometria 11, Coleccion de Problemas
Nivel: Educacion Secundaria, Academia, Preparatoria, Bachillerato, College
La figura muestra el triangulo rectángulo ABC, Si ángulo BAD = ángulo ACB = x y CD = 2BD, calcule x.
Ver mas:
Problema de Geometria 11, Coleccion de Problemas
Nivel: Educacion Secundaria, Academia, Preparatoria, Bachillerato, College
Suscribirse a:
Enviar comentarios (Atom)
al parecer este es el problema mas facil de todos,solo hay que aplicar semejanza de triangulos en ABD y ABC ;llamemos:
ResponderEliminarAB=b ,BD=a ,DC=2BD=2a
APLICANDO SEMEJANZA:
b/a=3a/b
b²=3a²...(1)
APLICANDO EL TEOREMA DE PITAGORAS en el triangulo ABD:
b²+a²=(AD)²
reemplazando (1):
3a²+a²=(AD)²
4a²=(AD)²
---->AD=2a
con esto nos damos cuenta que el triangulo ABD es notable
------->x=30
El triángulo ABD lo rotamos 180 alrededor del cateto AB se detremina untriángulo isósceles
ResponderEliminarluego observamos que todo la figura será un triángulo rectángulo entonces Ad resulta ser su menor mediana por lon tanto en el triángulo ABD es notable de 30 y 60 la respuesta será x=30
..si prologongamos AD hasta P, tal que AD=DP, de "P" bajamos la altura a BC la cual cae en "M", vemos que BD=DM=MC, unimos "P" con "C" podemos apreciar que los lados AP es a 2 como PC es a 1, podemos apreciar tambien que los angulos BAD,DPM,MPC son iguales "X"...ahora el angulo MCP mide 90-X, sumandole el angulo ACB "X" nos daria el angulo ACP --> 90-X+X=90, por lo tanto con la relacion obtenida anteriormente tenemos que el triangulo APC es el de 30 y 60, con los cual 2X=60.."X=30"
ResponderEliminarSe prolonga CB hasta un punto Q tal que QB=BD, se une A con Q, entonces el triangulo QAD es isóceles QA=AD. El triangulo QAC es rectangulo (QAC=90), entonces AD es la mediana relativa a la hipotenusa, con lo que 2QA=QC. El triangulo QAC es notable (30 y 60), por lo que x=30 .
ResponderEliminarSea CD=2a y BD=a.
ResponderEliminarCon respecto a AB se construye el triángulo APB simétrico de ABD, =>PB=BD, por lo cual el triángulo PAC será rectángulo. Se observa que D es punto medio de PC => AD:mediana relativa a la hipotenusa, de donde AD=a, luego el triángulo ABD es notable de 30° y 60°, por lo tanto x=30°
Solucion enviada por Alejandro Astudillo A. de Santiago, Chile en
ResponderEliminarProblema 11, Solucion 1
Aquí otro método: (sólo congruencias)
ResponderEliminar- Sea "M" punto medio de "DC". Se traza la altura "MP" ( "P" pertenece a "BC").
- Al unir mediante un segmento los puntos "D" y "P" se obtiene el "triángulo rectángulo BDP" (recto en "D")
- Se prolonga "PD" hasta que intersecte a la prolongación de "BA" en un punto "Q".
- Los triángulos:
*DPM
*PMC
*QAD
Son congruentes.
- Entonces "BD" se convierte en mediatriz del segmento "PQ"
- Por último se termina de completar ángulos y
x+2x = 90°
.: X = 30°
PD: me gustó la solución de "chamache"... mientras más creativo mejor, no le den mucho a las fórmulas.
Saludos.
Solucion en video del problema 11 enviada por Eder Contreras y Cristian Baeza de la Universidad Catolica de Valparaiso.
ResponderEliminar