viernes, 6 de marzo de 2009

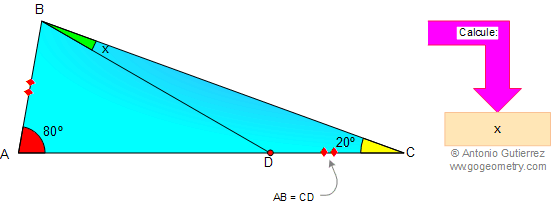
Problema 10: Triangulo, Ángulos, Ceviana, Trazos auxiliares

Problema propuesto
En la figura, AB = CD, ángulo A = 80º, y ángulo C = 20º. Calcule x.

Problema 10: Triangulo, Ángulos, Ceviana, Trazos auxiliares.

Ver mas sobre el problema 10 en:
gogeometry.com/geometria/p010_triangulo_ceviana_angulo.htm

Nivel: Educacion Secundaria, Academia, Preparatoria, Bachillerato, College
Posted by Antonio Gutierrez at 22:28
Labels: , , ,

4 comentarios:

  1. Anónimo22 de septiembre de 2009, 20:13

    vaya¡,este problema si estuvo un poco para pensar;bueno vamos a la solucion:

    -primeramente ubicamos un punto"E"(exterior relativo a BC)tal que al formar el triangulo BEC sea equilatero.

    -ahora llamemos: AB=a(pero como AB=CD entonces CD=a)y AD=b;en el triangulo ABC,completando angulos, el angulo ABC=80,entonces dicho triangulo es isoceles,BC=AC=a+b.Ahora el triangulo BEC es equilatero,entonces:BE=EC=BC=a+b

    -luego unimos los puntos "D" y "E"(¿para que?),para hacer congruencia con los triangulos ABC y DCE , en este caso seria L.A.L
    en ABC: Lado-a(AB) Angulo-80(ABC) Lado-a+b(BC)
    y en DCE:Lado-a(DC) Angulo-80(DCE) Lado-a+b(EC)

    -ya confirmando que los triangulos ABC y DCE son congruentes,procederemos a completar los lados:
    "en el triangulos ABC,al angulo 80(angulo ABC)se le opone el lado "a+b"(AC) , entonces en el triangulo DCE al angulo 80(angulo DCE)tambien se le debe de oponer el lado "a+b"(DE) >>>> DE=a+b

    -ahora en el triangulo DEC,al tener que:DE=a+b ,
    dicho triangulo seria isoceles,entonces el angulo EDC=80
    completando angulos,el angulo DEC=20,pero como el angulo BEC=60 >>>> el angulo BED=40

    -finalmente en el triangulo BED(que es isoceles por cierto porque:BE=ED=a+b),como el angulo:EBD=x+60
    >>> el angulo BDE=x+60(por ser triangulo isoceles).
    Ya bueno el resto es facil:
    en el triangulo BED:
    (angulo EBD)+(angulo BDE)+(angulo BED)=180
    reemplazamos:
    (x+60)+(x+60)+40=180
    2x=20 >>>>>>>>>>>>>>>>>> RPTA: x=10

    ResponderEliminar
  2. Antonio Gutierrez19 de octubre de 2011, 10:35

    Solucion enviada por Alejandro Astudillo A. de Santiago, Chile en
    Problema 1, Solucion 1

    ResponderEliminar
  3. Antonio Gutierrez26 de enero de 2012, 19:23

    Solucion en video del problema 10 enviada por Eder Contreras y Cristian Baeza de la Universidad Catolica de Valparaiso.

    ResponderEliminar
  4. Pedrim27 de junio de 2016, 17:24

    Esta es mi solucion:
    AC=BC, angulo ABC = angulo BAC = 80°
    Interno al triangulo ABD construimos un equilatero ABP, AP=PB
    Indirectamente estamos asumiendo que X es menor a 20°, de no ser asi llegariamos a una contradiccion
    Angulo PAC = 20°
    Angulo BCP = angulo ACP = 10° (APC es congruente con BCP caso L.L.L)
    Triangulo PAC es congruente con triangulo DCB (caso L.A.L.)
    por lo tanto X=10° (lo cual no contradice lo que asumimos sobre X)

    ResponderEliminar

Suscribirse a: Enviar comentarios (Atom)