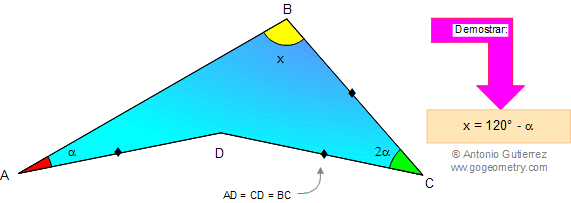
En la figura, AD = CD = BC, y el ángulo C es el doble del ángulo A. Demostrar que x = 120° - ángulo A.
Ver mas sobre problema 4 en:
gogeometry.com/geometria/p004_cuadrilatero_angulos_lados_iguales_trazo_auxiliar.htm
Nivel: Educacion Secundaria, Academia, Preparatoria, Bachillerato, College
Hola soy dante tengo 13 años.se traza la bisectriz en el triangulo BDC,que a la vez es altura, desde el vertice C y se prolonga hasta cortar a AB en E.Despues AED es congruente con DEC.El cuadrilatero BEDC seria un trapezoide simetrico.Entonces BEC=CED=DEA.Cada uno de estos angulos iguales suman 180, por eso van a ser igual a 60. En el triangulo BEC se aplica la suma de angulos internos y se obtiene lo que se quiere demostrar.Voy a seguir intentando los siguientes problemas.
ResponderEliminarHola,saludos a todos los que entran a esta grandiosa pagina,ya casi son 3 meses que no entro
ResponderEliminaraqui,pero bueno dejemo eso atras,ahora voy a retomar mi labor,intentando resolver los problemitas,bueno la explicacion que dio dante,es excelente y aprovechando la ocasion(cosa que no dije antes) para decirte que realmente me impresionas,que a pesar de tu edad ya sepas resolver este tipo de problemas Felicitaciones¡¡ , yo en cambio recien cumplo 16,y recien desde el año pasado aprendi a resolver problemas de este nivel,bueno vamos al problema :
1) Para comenzar trazamos las alturas CE y DF en los triangulos DBC y ABD respectivamente
2) Ahora como el triangulo DBC es isoceles,podemos decir que DE = EB = b verdad
3) Ahora completemos angulos,angulo FDA = 90 - a
("a" es alfa), EDC = 90 - a y DBC = 90 - a
4)Ahora si nos damos cuenta los triangulos AFD y DEC son congruentes por el caso LAL,verdad,
entonces en el triangulo DEC,como al angulo "alfa" se le opone un segmento que mide "b",entonces en el triangulo AFD al angulo "alfa" tambien se le debe de oponer un segmento que mida "b" verdad,entonces FD = b
5) Ahora si observamos el triangulo DFB es notable verdad,porque FD = b y DB = 2b,entonces
angulo FBD = 30
Entonces : x = 30 + 90 - a
---> x = 120 - a
Solucion en video realizado por Eder Contreras y Cristian Baeza en Problema de Geometria 4. Gracias Eder y Cristian.
ResponderEliminarSolucion enviada por Alejandro Astudillo A. de Santiago, Chile en
ResponderEliminarProblema 4, Solucion 1