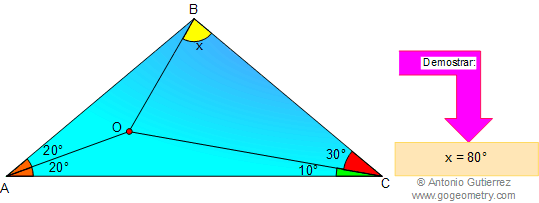
En un triangulo ABC, ángulo BAO = ángulo OAC = 20°, ángulo ACO = 10°, y ángulo OCB = 30°, Demostrar que el ángulo OBC = 80°.
Ver mas sobre problema 2 en:
gogeometry.com/geometria/p002_triangulo_angulos_trazo_auxiliar.htm
Nivel: Educacion Secundaria, Academia, Preparatoria, College
Basta aplicar el teorema de ceva (forma trigonométrica) a los ángulos que determinan las cevianas que pasan por los vértices del triángulo y el punto O, y sabiendo que el ángulo B=100, para obtener el resultado.
ResponderEliminarYo encontré una solución, pero me parece un poco compleja, bueno, aquí va: prolongamos AO hasta que se intersecte con BC en P, luego para aprovechar la bisectriz del ángulo BAC trazamos desde el vértice B una perpendicular a AP de modo que se intersecte con OP en R y con AC en Q, entonces el triángulo QAB es isósceles con base BQ, también por ángulo exterior se tiene que mےPOC=30° y mےAPB=60°, ahora trazamos QP, como BR=RQ se tiene que mےOPQ=60°, entonces si llamamos S a la intersección de PQ y OC, notaremos que el triángulo OPC es isósceles, además que mےOCP=60°, con lo cual PS sería también una altura, entonces, mےPSO=90° y también OS=SC; ahora, en el triángulo OQC se puede entender que mےQOC=10° (puesto que la altura QS es también mediana, con lo que el triángulo resulta isósceles), ahora, por ángulo exterior mےAQO=20°, pero como QAB y QOB con isósceles con base BQ, se tiene también que mےABO=20°, y nuevamente por ángulo exterior en el triángulo AOB se tiene que mےBOP=40°. Finalmente en el triángulo OPB tendríamos que 40°+60°+x = 180°, con lo que x=80°.
ResponderEliminarPor favor, si alguien tiene una solución menos engorrosa, publíquela :)
Hay una forma de resolver el problema aplicando trigonometría, (no se aplica cevas) no se hace ningún trazo auxiliar (se deja el gráfico tal y como está). El que desee que se lo envié, mi correo es rafaelcar22@hotmail.com.
ResponderEliminarel problema esta muy facil simplemente se forma un triangulo isosceles de esos dos angulos de 20°y a asi esa bisectriz seria una altura y de ahi chequealo y busca otro triangulo isosceles pequeño
ResponderEliminareso es todo.
*mi correo es :paxton93@hotmail.com
Hola,soy yo otra ves,al parecer la solucion
ResponderEliminarde Gabriel(como el mismo lo dice tambien),es
un poquito compleja,asi que yo propongo
una solucion,mas facil y entendible.
Para comenzar,prolongemos AB,hasta un punto "D",
tal que AD = AC,entonces el triangulo DAC,seria
isoceles,verdad.
Luego,si prolongamos AO,formaria con DC un angulo de 90º, verdad y a este punto de
interseccion,llamemosle que sea "E",luego
por angulo exterior,tendriamos de
que m< EOC = 30º y m< DBC = 80º,luego
completando angulos en el triangulo
rectangulo OEC,tendriamos de que m< BCE = 30º.
Luego,como el triangulo ADC es isoceles,su
altura caeria en el punto medio,verdad,entonces
DE = EC = b , luego como el triangulo OEC,
es notable por 30º y 60º,entonces OC = 2b
Finalmente,si nos damos cuenta,los triangulos
OCB y BCD,son congruentes,por el caso L.A.L ,
verdad.
Nota : los triangulos OCB y BCD,tienen un
mismo lado en comun que es BC)
Entonces en el triangulo BCD,como al segmento
que mide "2b",se le opone un angulo de 80º,
entonces en el triangulo OCB,al segmento que
mide 2b,tambien se le debe de oponer un
angulo de 80º,verdad.
--> x = 80º
Bueno eso es todo ¡¡
Saludos desde Lima - Peru
analice las formas escritas y vi q eran muy largas asi q aca les dejo un metodo cortisimo:
ResponderEliminar1ºtrazamos desde el punto O una ceviana hasta AC en un punto llamado P(p esta en AC ).Tal q m< POC =10.Ahora por suma de angulos externos m<OPA sea 20º entonces se forma un triangulo isosceles AOP.Ahora por congruencia :A 20 se le opone un lado llamado M al otro lado tmb M .entonces vemos q en el triangulo ABC es isosceles tambien .y por ultimo sumar los lados 20+20+20+X+30+10=180 X=80
analice las formas escritas y vi q eran muy largas asi q aca les dejo un metodo cortisimo:
ResponderEliminar1ºtrazamos desde el punto O una ceviana hasta AC en un punto llamado P(p esta en AC ).Tal q m< POC =10.Ahora por suma de angulos externos m<OPA sea 20º entonces se forma un triangulo isosceles AOP.Ahora por congruencia :A 20 se le opone un lado llamado M al otro lado tmb M .entonces vemos q en el triangulo ABC es isosceles tambien .y por ultimo sumar los lados 20+20+20+X+30+10=180 X=80
Ruben que criterio de semejanza de triangulos aplicas para que la medida ABO sea 20, no me convence
ResponderEliminarEl triangulo ABC es isoceles, AB=BC. Sea la incognita "x". Exteriormente al triangulo y relativo al lado BC se ubica un punto T, talque TC=AO y el angulo TCB=20 con ello logramos que los triangulos AOB y BCT sean congruentes, con lo que BO=BT y el angulo ABO=CBT, entonces en angulo OBT=100. En el triangulo AOC se traza la ceviana OP (P en AC) tal que AO=OP,con lo que el triangulo OPC es isoceles ( AO=OP=PC ). Se une P con T formandose el triangulo equilatero PTC, entonces en angulo OPT)=100. Ademas, el triangulo OPT es isoceles con lo que el angulo POT=40, entonces los puntos A,O y T son colineales. Recordemos que por la congruencia que hemos buscado el triangulo OBT es isoceles, con lo que el angulo BOT=40, Habiamos denotado al angulo OBC como "x". por lo que el angulo ABO=100-x. pero por angulo exterior los angulos ABO + BAO = BOT. Osea, 100-x + 20 = 40, por lo tanto x=80.
ResponderEliminarAnònimo aclaro el criterio de semejanzo de Rùben al demostrar que el àngulo ABO=20º, el cual queda solucionado el problema.
ResponderEliminarAqui les traigo otra solución.
ResponderEliminar1)prolongamos AB has ta "P", tal que AP=AC,--> el △APC es isósceles(de base PC). En el △APC, completando ángulos, se tiene que mm△OPC es equilátero, de donde PC=a y m m<BOC=70°.
5)△BOC: 30°+70°+x=180°
Por lo tanto x=80°.
la solucion de cesar cruz es la mas adecuada
ResponderEliminarProfesor gutierrez, podría buscar una forma de que se pudiese usar latex o algo así :P
ResponderEliminarExcelente César, me gustó esa resolución.
ResponderEliminar=D
me gusta este tipo de trazos auxiliares, te hace pensar y razonar, aunque me gusto el criterio del cuarto anónimo por lo rápido que fue...chido un punto para ti....y porfas envíen mas problemas de estos que soy fanático e ídolo de la geometría...!
ResponderEliminarSolucion en video realizado por Eder Contreras y Cristian Baeza en Problema de Geometria 2. Gracias Eder y Cristian.
ResponderEliminarSolucion enviada por Alejandro Astudillo A. de Santiago, Chile en
ResponderEliminarProblema 2, Solucion 1
Yo tengo una solución: Primero prolonga AB hasta el punto E de tal forma que AE=AC, luego obtenemos el triángulo isoceles AEC y la recta medriatriz AD respecto al lado CE. Completando ángulos obtenemos <COD=30, <BCE=30, <BEC=70 y <EBC=80. Trazamos OE y obtenemos el triángulo equilatero COE, y por propiedad BC es la recta mediatriz de dicho triángulo equilatero, entonces tenemos que <OBC=<EBC de donde obtenemos x=80
ResponderEliminar