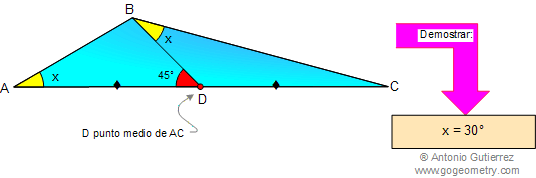
En un triangulo ABC, BD es la mediana relativa a AC, los ángulos A y DBC son iguales. Si el ángulo ADB mide 45°, demostrar que el ángulo A mide 30°.
Ver mas:
Problema 1
Lista de problemas en Espanol
Lista completa de problemas en Ingles
Nivel: Educacion Secundaria, Academia, Preparatoria, College
Hola trate de realizarlo pero llego a contradicciones
ResponderEliminar¿?
Como el àngulo BDC = 135 puedo trazar una recta de D que intersecte a BC en T de forma que el àngulo BDT=45. Por criterio AAL el triangulo ABD seria congruente a BTD.
A lo cual llegaria que BTD es isosceles, pero por suma de àngulos llegaria a contradecir que la suma de los angulos da 180.
Me podrìas decir en que me equivoco??
Ya que estuve realizando el problema 5 pero tambien llego a contradicciones similares
PDT. Zoe.b19@gmail.com
Gracias por la pregunta.
ResponderEliminarA los triangulos ABD y BTD no se les puede aplicar el criterio AAL porque no tienen un lado congruente, solo tienen angulos iguales, o sea son semejantes.
Hola soy Dante tengo trece años. AD=DC=a .se prolonga AB y se traza CE perpendicular a AB tal que CEB es igual a 90. En el triangulo ABD, DBE es igual a 45+x por angulo exterior, como DBC ya es x CBE tiene que ser igual a 45.
ResponderEliminarBE=EC=b y BC es b√2 por triangulo notable de 45.Despues ABC es semejante con BDC.
Entonces: b√2/a=2a/b√2
al final queda a=b
Ahora el triangulo AEC es rectangulo notable de treinta y 60.por lo tanto:
X=treinta
voy a intentar hacer los demas problemas.
hola amigo eh cual es la semejanza en los triangulos ABC y BDC.
EliminarGracias por la pregunta.
ResponderEliminarA los triangulos ABD y BTD no se les puede aplicar el criterio AAL porque no tienen un lado congruente, solo tienen angulos iguales, o sea son semejantes.
Gracias por la aclaración es que se nos habia dado el criterio ALA incorrecto.
Realizado el 5, el 3
Hola Gracias por responder. Se habia escrito mal el Críterio ALA.
ResponderEliminarRealizando los problemas.
Esta buena la página!
Yo encontré otra solución, se circuscribe al triángulo ABD de modo que el lado BD sea tangente en B a dicha circunferencia, se puede hacer eso por las posiciones del ángulo x, luego hacemos AD = DC = a, entonces por relaciones métricas en la circunferencia BC^2 = AC.DC, con lo que BC = a√2, podemos notar que el ángulo ABC mide 135°(puesto que el ángulo ABD mide 135°-x)y finalmente aplicamos ley de senos en el triángulo ABC: 2a/sen135° = a√2/sen x, resultando sen x = 1/2, entonces x = 30°. Quiero mencionar también que no se me ocurrió la solución que planteó Dante, le estuve dando vueltas al problema pero no pude demostrar que, según las variables que planteó, a = b, noté la semejanza pero no se me ocurrió aplicarla, bien por el muchacho, saludos.
ResponderEliminarla cosa es hacerlo solo por geometria pero igual vale
ResponderEliminarMe confundí al escribir, el no tiene sentido decir que el lado BD sea tangente en B a la circunferencia exterior, quise decir que BC sería tangente en B a dicha circunferencia, mil disculpas.
ResponderEliminarEu encontrei outra solução:
ResponderEliminarEu traçei uma reta perpendicular partindo do ponto B em encontro com o lado AC no ponto M, e tracei uma paralela a esta reta, que toca o lado BC em H e AC em D.
Fiz semelhanças nos triângulos BDH e ABD, depois fiz semelhanças nos triângulos BCM e HDC, depois caí numa equação do 2º grau: y² + y(-2c) - 2c²
Sendo que AD=DC=y e MD=MB=c
No fim achei y=c + c(raiz de 3)e descobri que AM=c(raiz de 3)
e o triângulo ABM é egípcio, logo x=30º
si son congruentes en la resolucion de dantebazan se aplica el caso AAA! los angulos son x; x - 45; 135. =S!
ResponderEliminarHola soy Martín aca les dejo un problema:
ResponderEliminarSe tiene un triangulo ABC, se traza la mediana AD
si m<ABC=90+X,m<BAD=2X y m<BCA=2X, hallar "X"
si kieren saber como se resualve les dejo mi correo: tinmar_moralitos@hotmail.com
la solución de dante es buena. Yo les planteo otra solución.
ResponderEliminar1)Sea AD=DC=a, por el teorema de las antiparalelas, se concluye en el triángulo ABC que BC=a√2.(se demuestra por semejanza de triángulos dado que los triángulos ABC y BDC son semejantes)
2)se observa que el triángulo BDC es obtusángulo, por lo cual su circuncentro "O" está en la región exterior relatica a BC. Por propiedad de circuncentro,BO=OC=OD=b, además la mmBC=b√2, pero en el paso 1 se determino que BC=a√2, por lo cual a=b.
4) Para terminar, el triángulo ODC es equilátero, entonces 2x=60°.
Por lo tanto x=30°
Solucion en video realizado por Eder Contreras y Cristian Baeza en Problema de Geometria 1. Gracias Eder y Cristian.
ResponderEliminarSolucion enviada por Alejandro Astudillo A. de Santiago, Chile en
ResponderEliminarProblema 1, Solucion 1
Solución Problema 1:
ResponderEliminarhttps://www.pinterest.es/pin/616289530266320595/