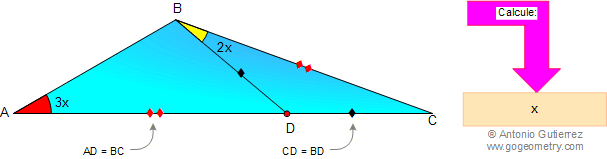
En la figura, AD = BC, BD = CD, ángulo A = 3x, y ángulo DBC = 2x. Calcule x.
Ver mas sobre problema 5 en:
gogeometry.com/geometria/p005_triangulo_angulo_ceviana_trazo_auxiliar.htm
Nivel: Educacion Secundaria, Academia, Preparatoria, Bachillerato, College
Hola soy dante tengo trece años.como BD=DC,BDA seria 4x.En el interior del triangulo ABD se ubica el punto E tal que BAE=x ,EAD=2x ,BDE=EDA=2x.Entonces AED es congruente con BDC por ALA, entonces BD=DC=AE=ED.En el triangulo isosceles BDE se va a trazar la bisectriz q a la vez seria altura y se va a prolongar hasta cortar en F a AB,entonces como AFE es congruente con EFD y EFBD es un trapezoide simetrico, los angulos AFE,EFD y DFB serian iguales y sumarian 180 por eso cada uno es igual a 60.como AFDE es un cuadrilatero no convexo, AED es igual a x+60+60+x.ahora en el triangulo AED 2x+x+60+60+x+2x=180, por lo tanto x=10 grados. E intentado resumirlo de la manera que me ha salido pero creo q hay otra mas fácil.bueno eso es todo.
ResponderEliminar1º se suman los dos internos 2x + 2x =4x verdad... ahora el triangulo BDC y ABD tienen un lado en comun verdad entonces inscribes ese triangulo en ABD de modo q te van a salir dos angulos en relacion de 1 a 2...y aplicas propiedad en un triangulo concavo (triangulo en forma de boomerang) cuando dos angulos estan en relacion de 1 a 2 el tercer angulo sera 120-2x.ahora igualamos 3x+2x+2x+120-2x=180 X=10
ResponderEliminarSolucion en video realizado por Eder Contreras y Cristian Baeza en Problema de Geometria 5. Gracias Eder y Cristian.
ResponderEliminarSolucion enviada por Alejandro Astudillo A. de Santiago, Chile en
ResponderEliminarProblema 5, Solucion 1