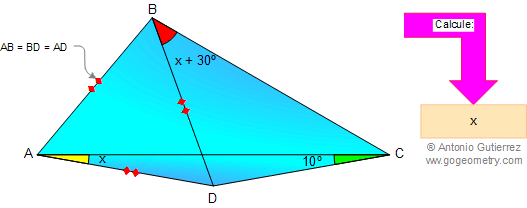
En la figura, AB = BD = AD, ángulo ACD = 10º, ángulo CAD = x, y ángulo CBD = x + 30º. Calcule x.
Ver mas sobre el problema 9 en:
gogeometry.com/geometria/p009_triangulo_angulo_equilatero_trazo_auxiliar.htm
Nivel: Educacion Secundaria, Academia, Preparatoria, Bachillerato, College
Para los que desean saber como se hace este problema grafiquen lo que voy explicando paso a paso ok?
ResponderEliminar.Primeramente cortamos al angulo DBC en x y 30 grados(dicho segmento que corta al angulo DBC se intersecta con AC en un punto "E"),ahora rapidamente vemos que el angulo BEA=60(porque completando angulos el angulo BCA=30)
.Ahora cortamos al angulo ABD en x y (60-x) grados(dicho segmento que corta al angulo ABD se intersecta con AC en un punto "F"),ahora si nos damos cuenta el triangulo FBE es equilatero >>> el angulo BFA=120
.Llamemos:FB=b(pero como el triangulo FBE es equilatero,todos sus lados deben medir la misma longitud)>>BE=b;ahora teniendo esto unimos los puntos "D" y "E"(¿para que?),para hacer congruencia con los triangulos ABF y DBE(la ves o no la ves).En este caso seria L.A.L.
En el triangulo ABF:Lado(AB)-Angulo(x)-Lado(b)
En el triangulo DBE:Lado(BD)-Angulo(x)-lado(b)
(Recuerda que AB=BD porque el triangulo ABD es equilatero)
Ya confirmando que los triangulos son congruentes,procedemos a completar los lados y angulos(ok?)
"(en el triangulo ABF)Como al segmento AB se le opone el angulo de 120,(en el triangulo DBE)entonces a BD tambien se le debe de opones el angulo de 120"
>> el angulo BED=120 >> el angulo AED=60
"(en el triangulo ABF)Como al angulo "x" se le opone el segmento "a"(llamemos a AF=a),(en el triangulo DBE)entonces al angulo "x" tambien se le debe de oponer el segmento "a"(verdad?)"
>> DE=a
.Miremos el triangulo BEC, es isoceles(verdad?),entonces BE=EC,pero como BE=b >> EC=b
.Ahora en el triangulo DEC(el angulo AED=60 es angulo exterior de dicho triangulo),el angulo EDC=50
.Ahora procederemos a hacer una ultima congruencia de triangulos(ok?,pero tu diras ¿cuales?,mira el grafico y date cuenta cuales son),si la vistes bien por ti,pero si no atento aca(ok?).Los triangulos congruentes serian ABF y DEC.Caso L.A.L.
En el triangulo ABF:Lado(a)-Angulo(120)-Lado(b)
En el triangulo DEC:Lado(a)-Angulo(120)-Lado(b)
Ya confirmando que los triangulos son congruentes,procedemos a completar los lados(ok?)
"(en triangulo ABF)Como al angulo 120 se le opone el segmento "m"(llamemos a AB=m),(en el triangulo DEC)entonces al angulo 120 tambien se le debe de oponer el segmento "m" " >>> DC=m
Recuerda que el triangulo ABD es equilatero:
>> AB=BD=AD=m;pero por congruencia habiamos concluido que DC=m;ahora si miramos el triangulo ADC es isoceles(puesto que AD=DC=m)
FINALMENTE:
>> x=10
P.D:Otro problema que tambien llamo mi atencion(me gusta resolver este tipo de problemas)
Solucion enviada por Alejandro Astudillo A. de Santiago, Chile en
ResponderEliminarProblema 9, Solucion 1
Aquí una solución más sencilla:
ResponderEliminar- Prolongar "BD" hasta el punto "P" siendo el ángulo DAP igual a 30° y por lo tanto el cuadrilátero "ABCP" inscriptible en una circunferencia.
- Completamos ángulos y notamos que: BCP=90°
- Para esto ABP sería un triángulo rectángulo y "D" sería punto medio de "BP" (BD=DP)
- Entonces se cumple que:
BD=DP=CD
- En el triángulo BCD:
* BCD = DBC = 30° + x = 40°
.: X = 10°
Solucion en video del problema 9 enviada por Eder Contreras y Cristian Baeza de la Universidad Catolica de Valparaiso.
ResponderEliminarCuales son los criterios para realizar trazos auxiliares, alguna información para complementar
ResponderEliminarQue no altere tus hipótesis.
EliminarHola, me llamo Pedro M
ResponderEliminarMi solucion es como sigue:
Construimos el triangulo equilatero ACE de modo que B es un punto interno de dicho triangulo.
El angulo BAE = x = angulo BEA (pues BC es bisectriz y mediatriz del angulo ACE)
BA=BE pues triangulo ABE es isosceles
Triangulo ABE es congruente con triangulo ADC (caso L.A.L.)
X=10°