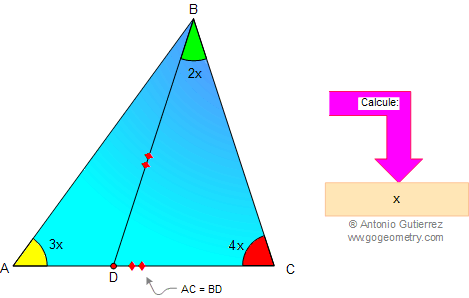
En la figura, AC = BD, ángulo A = 3x, ángulo BCD = 4x, y ángulo CBD = 2x. Calcule x.
Ver mas sobre problema 7 en:
gogeometry.com/geometria/p007_triangulo_angulo_ceviana_trazo_auxiliar.htm
Nivel: Educacion Secundaria, Academia, Preparatoria, Bachillerato, College
Prolonga AC até um ponto J, tal que, CJ é igual a AD. Depois, percebemos que DB=DJ logo o ângulo CJB= 3x e JBC=x. Ao observarmos o Triângulo ABJ, vemos que AB=BJ, logo podemos provar uma congruência entre ADB e JCB, pelo caso LAL
ResponderEliminarHola,antes cuando explicaba los problemas lo hacia paso a paso,pero creo que eso ya no es necesaio porque aqui la mayoria ya debe saber conceptos basicos de geometria,ahora vamos al problema :
ResponderEliminar1) Prolongamos AC hasta un punto "E" tal que
el angulo BEC = 3x y AB = BE
2) Ahora llamemosle a AD = a y a DC = b,pero
como AC = BD --> BD = a + b,pero como el triangulo DBE es isoceles --> DB = DE --> CE = a
3) Ahora si nos damos cuenta los triangulos DAB y CEB son congruentes po el caso LAL,entonces en el triangulo DAB,como al angulo "3x" se le opone un segmento que mide "a + b",entonces en el triangulo CEB,al angulo "3x" tambien se le debe de oponer un segmento que mide "a + b",entonces CB = a + b
4) Ahora si nos damos cuenta el triangulo DBC es isoceles,entonces el angulo BDC = BCD
entonces el angulo BDC = 4x,luego en el
triangulo DBC : 4x + 2x + 4x = 180
---> x = 18
Solucion enviada por Alejandro Astudillo A. de Santiago, Chile en
ResponderEliminarProblema 7, Solucion 1
Solucion en video enviado por Eder Contreras en
ResponderEliminarSolucion en video
Tengo otra solución:
ResponderEliminar- Trazar la ceviana "DE" ( "E" pertenece a "AB" ), tal que el "ángulo ADE" mida "3x" por lo que: AE=DE.
- Trazar el segmento "EC".
- Se notará que los triángulos "BDE" y "CAE" son congruentes (Caso LAL).
- Se observa entonces que EB=EC
- Completando ángulos en el "triángulo BEC":
*BEC=4x
*BCE=3x
*EBC=3x
- Por lo tanto:
4x+3x+3x=180
.: X = 18°