viernes, 6 de marzo de 2009

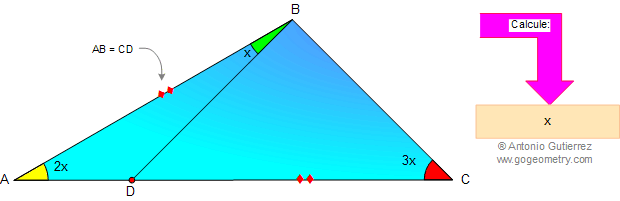
Problema 6: Triangulo, Ángulos, Ceviana, Trazos auxiliares

Problema propuesto
En la figura, AB = CD, angulo A = 2x, y angulo BCD = 3x. Calcule x.

Problema 6: Triangulo, Ángulos, Ceviana, Trazos auxiliares.

Ver mas sobre problema 6 en:
gogeometry.com/geometria/p006_triangulo_angulo_ceviana_trazo_auxiliar.htm

Nivel: Educacion Secundaria, Academia, Preparatoria, Bachillerato, College
Posted by Antonio Gutierrez at 14:38
Labels: , , ,

5 comentarios:

  1. Anónimo23 de octubre de 2009, 20:55

    Para los que desean saber como se hace este problema grafiquen lo que voy explicando paso a paso ok?
    .A simple vista el angulo BDC=3x(con esto demostramos que el triangulo DBC es isosceles)

    .Ahora desde el vertice D trazamos la ceviana interior DE en el triangulo ABD,tal que el angulo AED=2x(con esto demostramos que el triangulo AED es isosceles) >>> el angulo EDB=x(con esto demostramos que el trianglo EDB es isosceles)

    .Llamemos: EB=a >> ED=a(por ser isosceles)y AD=a(por ser isosceles)

    .Ahora ubicamos un punto F en el triangulo DBC,tal que DF=a y el angulo FDC=2x >> el angulo BDF=x(completando angulos) y unimos los puntos"F" y "C" y los puntos "F" y "B" y por ultimo los puntos "F" y "E"(tal que la interseccion de los segmentos EF y DB sea un punto "G")

    .A simple vista en el triangulo DEF,el angulo DGF=90(por ser isoceles) y EG=GF(por ser isoceles el triangulo DEF la altura DG seria la mediatriz de dicho triangulo) >> EB=FB con esto deducimos que FB=a(por ser isoceles),ahora como se habran dado cuenta en el triangulo EBF,BG actua como mediatriz de dicho triangulo >>> el angulo GBF=x

    .Ahora veamos los triangulos DAB y FDC(son congruentes ¿verdad?),cuyos lados congruentes son: (caso L.A.L.)
    AB-angulo BAD-AD=a
    DC-angulo FDC-FD=a
    ya habiendo comprobando que los triangulos son congruentes,completemos los lados y angulos faltantes,"(en el triangulo DAB)como al segmento AD=a se le opone el angulo x >> (en el triangulo FDC)al segmento DF=a tambien se le debe de oponer el angulo x(¿verdad?)" >> el angulo FCD=x y el angulo FCB=2x(completando angulos)

    .Llamemos a DG=b >> GB=b(por ser isoceles el triangulo DEB),DB=DG+GB(a simple vista) >> DB=b+b --> DB=2b >> BC=2b(por ser isoceles el triangulo DBC)

    .Uhmm¡ Se nos olvido completar un lado al momento de hacer la congruencia(no te diste cuenta),pero bueno nunca es tarde hagamoslo ahora ok?
    "(en el triangulo DAB)si al angulos DAB=2x se le opone el segemnto DB=2b >> (en el triangulo FDC)al angulo FDC=2x tambien se le debe oponer el segmento "2b" >> FC=2b

    .Ya casi acabamos no te aburras ok?;en el triangulo FBC(si te habras dado cuenta es isoceles),el angulo FBC=al angulo BFC >> el angulo FBC=90-x

    .Finalmente llegamos a la respuesta(ehh);en el triangulo DBC, el angulo DBC=90(¿verdad?) >> dicho triangulo es rectangulo

    >> (el angulo BDC)+(el angulo DCB)=90
    reemplazemos:3x+3x=90
    ----> x=15
    P.D:estuvo muy interesante el problema,me gusto

    ResponderEliminar
  2. Anónimo23 de noviembre de 2010, 17:11

    el METODO CORTOO:
    1ºx + 2x =3x verdad
    2ºvemos un t.isosceles DBC
    3ºcomo el triangulo ABD y DBC tienen un lado en comun trasladamos todo el triangulo ADB en el isosceles
    4º vemos de nuevo el triangulo boomerang el cual los angulos son de 2 a 1 entonces DBC es 120-2x
    SOLO FALTARIA:
    3x+120-2x+3x=180 x=15

    ResponderEliminar
  3. Antonio Gutierrez4 de septiembre de 2011, 15:33

    Solucion en video realizado por Eder Contreras y Cristian Baeza en Problema de Geometria 6. Gracias Eder y Cristian.

    ResponderEliminar
  4. Antonio Gutierrez8 de septiembre de 2011, 23:15

    Solucion enviada por Alejandro Astudillo A. de Santiago, Chile en
    Problema 6, Solucion 1

    ResponderEliminar
  5. Luis Montenegro28 de diciembre de 2021, 10:11

    https://www.pinterest.com/pin/616289530266310298/

    Prolongas DC a la derecha hasta formar un Triángulo isósceles, luego prolongas del nuevo triángulo de la derecha desde B hacia arriba a la izquierda hasta que se forme un Triángulo equilátero y se forma un Triángulo rectángulo (propiedad de la mediana de dicho triángulo)

    ResponderEliminar

Suscribirse a: Enviar comentarios (Atom)