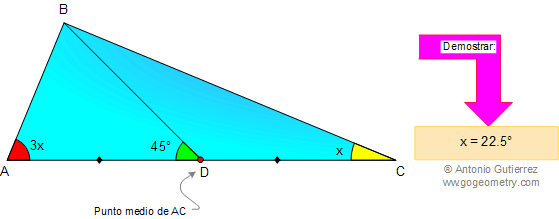
En un triangulo ABC, BD es la mediana relativa a AC. Si el ángulo BAC es el triple del ángulo C, y el ángulo ADB = 45°, demostrar que el ángulo C = 22.5°.
Ver mas sobre problema 3 en:
gogeometry.com/geometria/p003_triangulo_angulos_mediana_trazo_auxiliar.htm
Nivel: Educacion Secundaria, Academia, Preparatoria, Bachillerato, College
muy bueno el problema deja cosas en claro
ResponderEliminarmuchas gracias por publicarlo
.bueno tratare de explicar este problema lo mas breve posible ok?(pero entendible), porque tengo que hacer otras cosas
ResponderEliminar.en el triangulo ABD ubicamos un punto "E",tal que la med.del angulo BEA=3X,ahora en dicho triangulo trazamos la altura BH(que caeria en el punto medio),llamemos AH=a >> HE=a
ED=b,en el triangulo BHD(es notable)>>HD=HB=a+b
.ahora ubicamos un punto "F" en BC,tal que la med.del angulo EFB=2x,dicho angulo es exterior al triangulo EFC >> la med.del angulo FEC=x(completando angulos la med.del angulo EBC=2x,entonces el triangulo BEF es isoceles >> BE=EF),ahora en el triangulo EFC,trazamos la altura FG(que caeria en el punto medio)
ahora como AD=DC(por dato)AD=2a+b >> DC=2a+b,pero como ED=b >> EC=2a+2b(entonces la altura FG corta a EC en EG=a+b y GC=a+b),>> DE=a.
ahora rapidamente miremos el triangulo HBE(catetos: a+b y a,hipotenusa=m)y el triangulo EFG(catetos: a+b y FG ,hipotenus=m(porque el triangulo BEF es isoceles)),ya despues de ver los triangulos nos damos cuenta que:FG=a(por teorema de pitagoras).
ahora por ultimo los triangulos HBE y EFG son congruentes(caso L.A.L)
HBE--->lado:a+b(HD) ,angulo=90(BHD) ,lado:a(HE)
EFG--->lado:a+b(EG) ,angulo=90(EGF) ,lado:a(FG)
"en EFG ,como al segmento "a"se le opone el angulo "x",>> en el triangulo HBE al segmento "a" tambien se le debe de oponer el angulo "x".Finalmente en el triangulo HBE:
3x+x=90 >> 4x=90
-----> x=22,5
P.D: ya lo habia hecho hace como 3semanas aprox. ,solo que no tenia tiempo para publicarlo
metodo el CORTO:
ResponderEliminar1º partiendo del punto "D" traza una perpendicular hacia arriba intersectando en E(E esta en BC)traza de A hacia E.
2º para q hicimos eso:para formar una mediatriz miren:en el triangulo AEC
3º el angulo BDE es 45.
4ºel angulo EAD es "X" entonces BAE es 2x.
ahi vemos una "corbata" q es ABDE el cual rebotan sus angulos siendo 2x=45 x=22.5
En la solución de Anónimo falta indicar el porqué se cumple el rebote en la "corbata".Eso se cumpliría si el cuadrilátero ABED fuese inscriptible
ResponderEliminar1)m 135°-3x=45-x, de donde x=45, lo cual es absurdo ya que al reemplazar ese valor en m<EBD nos daría 0°.
* con eso la única posibilidad es que sea inscriptible
PODRIA EXPLICAR UN POCO MAS CORTO
ResponderEliminarsi debe explicar que es el cuadrilatero inscriptible
EliminarSolucion en video realizado por Eder Contreras y Cristian Baeza en Problema de Geometria 3. Gracias Eder y Cristian.
ResponderEliminarSolucion enviada por Alejandro Astudillo A. de Santiago, Chile en
ResponderEliminarProblema 3, Solucion 1
LA solucion publicada en youtube, ya que asume que b es igual a 3 alfa, y esos es falso con los datos del problema.
ResponderEliminarAhí claramente Cristian dijo "-->desarrollando<-- este sistema, se obtiene la siguiente solución"
EliminarSi tomas la primera relación y la multiplicas por 3, obtienes 3b+3x=135, luego la restas con la primera obteniendo a-3b=0, luego a=3b.
Más atento para la próxima.
Saludos.
El cuadrilátero ABED es inscriptible si se cumple que el angulo en B o sea m<ABE es de 90 grados, con centro de la circunferencia en el punto medio de AE, ya que en un cuadrilátero inscriptible los ángulos opuestos son suplementario (m<ADE + m<ABE = 180 y m<ADE = 90 por construcción, por lo tanto m<ABE seria 90 grados), lo que no se ha demostrado.
ResponderEliminarEl demostrar lo anterior nos daría como resultado que 3x+x=90...............implica x=22.5
De otra manera, demostrando que la mediana BD=AD=DC cumpliendo con el teorema de la mediana respecto a la hipotenusa es igual a la mitad de la hipotenusa, lo que tampoco se ha demostrado.