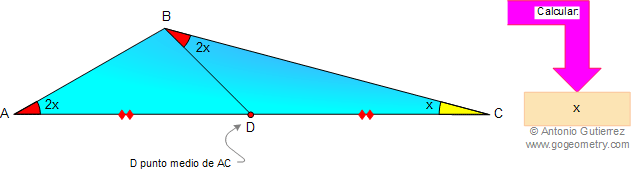
La figura muestra el triangulo ABC, ángulo C = x, ángulo A = ángulo CBD = 2x, y D es punto medio de AC. Calcule x.
Ver mas:
Problema de Geometria 14, Coleccion de Problemas
Nivel: Educacion Secundaria, Academia, Preparatoria, Bachillerato, College
domingo, 26 de abril de 2009
Problema 14: Triangulo, Ángulos, Mediana, Congruencia
Problema propuesto
La figura muestra el triangulo ABC, ángulo C = x, ángulo A = ángulo CBD = 2x, y D es punto medio de AC. Calcule x.
Ver mas:
Problema de Geometria 14, Coleccion de Problemas
Nivel: Educacion Secundaria, Academia, Preparatoria, Bachillerato, College
La figura muestra el triangulo ABC, ángulo C = x, ángulo A = ángulo CBD = 2x, y D es punto medio de AC. Calcule x.
Ver mas:
Problema de Geometria 14, Coleccion de Problemas
Nivel: Educacion Secundaria, Academia, Preparatoria, Bachillerato, College
Suscribirse a:
Enviar comentarios (Atom)
bueno ya me salio,pero para que no se maten pensando les dare la idea ok?
ResponderEliminarPaso 1:
en el triangulo ABC aplican semejanza de triangulos y tendran una relacion entre sus lados
Paso 2:
prolonguen CA hasta un punto "E" tal la medida del angulo BCA sea igual al de BEA y en AD ubiquen un punto "F" tal que el angulo BFD sea igual al de BDF
Paso 3:
En EBF apliquen el teorema de la bisectriz interior y obtendran AF en funcion a los lados que obtuvieron en la primera semejanza que hicimos
Paso 4:
apliquen semejanza en EBF y obtendran algo que les ayudara en el paso final
Paso 5 y ultimo:
apliquen ley de cosenos en BDC y con lo que obtuvieron en el paso 4 les saldra el coseno del
angulo BDC(dicho sea de paso es notable),hallando dicho angulo les saldra "x"
BUENO SI NO ENTENDIERON ME LO HACEN AVISAR HACIENDO UN COMENTARIO AQUI,DICIENDO QUE PARTE DE LA SOLUCION LES PARECE DUDOSO
P.D: despues les dire cuanto sale "x" primero piensen un poco igual que yo
Hola,yo soy el de arriba,disculpen si nos les dije cuanto salia el angulo "x",la respuesta
ResponderEliminares x = 15,pero despues de 3 meses que coloque esa
respuesta,ahorita recien que lo acabo de hacer otra ves,lo hice por otra forma,ya no por semejanza ni ley de cosenoa,como lo hice anteriormente,veamos :
1) Para comenzar en el triangulo BDC,trazamos la ceviana interior DE,tal que el angulo BED=2x
--> el angulo EDC = x,luego ubicamos un punto interior "F" en el triangulo ABD,talq ue el angulo FAD = al angulo FDA = x,ahora si nos damos cuenta,los triangulos AFD y DEC son congruentes por el caso ALA verdad,entonces :
DE = EC = a(en el triangulo DEC),pero como
BD = DE y DE = a --> BD = a,pero como dichos triangulos son congruentes,entonces :
AF = FD = a
2) Ahora completando angulos tenemos que el angulo BAF = x y el angulo BDF = 2x
3) Finalmente si nos damos cuenta el cuadrilatero concavo ABDF,es una propiedad verdad,entonces el angulo ABD = 120 - x
(esta propiedad esta como problema 4 de esta pagina y ademas esta demostrada por dante y por mi)
4) Ahora en el triangulo ABD ,tenemos :
2x + 120 - x + 3x = 180
4x = 60
--> x = 15
De Gabo:(FF)AYACUCHO
ResponderEliminarBueno lo primero para resolver este problema es construir un PARALELOGRAMO, para esto trazamos perpendiculares a los lados AB Y BC.
Segundo, dentro del triangulo ABC construimos un triángulo isóceles APC (los angulos iguales deben ser de medida x, así el angulo A se divide en dos angulos de igual amplitud)
Tercero, se traza la mediatriz en el triángulo ABC, esta debe pasar por P y debe chocar en el lado paralelo a ABC en Q(EN el paralelogramo el punto opuesto a B lo llamaremos D, y el punto de interseccion de diagonales: O, este debe interceptar con la mediatriz)
Cuarto, trazamos el segmento BQ; esto nos ayudara a ubicar cuadrilateros inscriptibles, y claro a ubicar los angulos restantes con funcion a X;
angulos: QPC,5X;CQD,2X;BQD,2X;BQA,3X;BQP,2X;DOC,3X;DBX,2X;APB,2X.
FINALMENTE:en el triangulo rectangulo formado por la porcion de la mediatriz de ac y ao (triangulo AOQ) 5x+6x=90; entonces X=15
Solucion enviada por Alejandro Astudillo A. de Santiago, Chile en
ResponderEliminarProblema 14, Solucion 1
Solucion en video del problema 14 enviada por Eder Contreras y Cristian Baeza realizado en el Instituto de Matemáticas (IMA) de la Pontificia Universidad Católica de Valparaiso (PUCV), Chile.
ResponderEliminarEsta es mi solucion:
ResponderEliminarhttps://mega.nz/#!xgpVwCpZ!bWAXmTVbp3s4_64N4HJusVscCW85NxLPmdHpw7BEbeU
Pedro Miranda